再也不怕秃顶？Digital Mike头发制作及渲染的深度揭秘

头发的生长和渲染技术是一大亮点，这是UE4团队首次用成熟的电影毛发制作流程来制作实时交互内容。毛发渲染技术中的基于物理双散射模型（dual scattering）是由腾讯团队开发的。这个模型也是首次集成到实时渲染引擎中来解决毛发的间接光照问题。电影和游戏的制作流程有很大的差异，很多电影技术都是高度依赖电影制作流程的，但是通过Epic和腾讯团队共同努力成功地将这些技术引入到实时交互内容的制作流程中来。整个过程中所积累技术和经验是值得推广和分享的。

【实时渲染系列专题】

Part1：SIGGRAPH 2017｜迄今为止最高品质实时数字人

Part2：跨越恐怖谷—实时渲染的突破和虚拟角色的诞生

Part3：Digital Mike头发制作及渲染的深度揭秘

后续文章陆续推出中

本文作者：腾讯互娱IEG - NEXT研发中心 高级工程师 ganggwang(王刚)

1. 概要

文章主要介绍在SIGGRAPH 2017 VR Village中展示的最新数字人研究技术展示MEETMIKE的头发制作流程和渲染流程。整体效果已经接近照片级渲染效果。这也是制作团队首次引入由Disney发明的电影制作毛发生长工具XGen来制作发型。毛发的渲染使用了基于物理真实的Marschner模型。

如上图所示，总共有440000三角形被实时渲染，这其中75%都是头发的模型。UE4用宽度非常细的一段段细长的四边形来代表头发曲线，毛发的宽度只有像素大小的几分之一，这使得整个图形光栅化过程的负担都很重。但是这样的渲染资源的消耗也带来的品质的大幅提升。一丝丝的头发效果可以展现在观众的眼前，并且每帧的渲染时间控制待VR所要求的9ms之内。

2. 毛发生长流程

传统的游戏制作毛发技术会选择用插片的方式来代替一丝丝的头发形状，每一片插片代表一层头发，然后用贴图控制Alpha通道来控制每根头发的形状。这样做的优点是性能符合游戏的需求。缺点是毛发生长的形状有限制，不可能制作出任意形状的头发模型。

电影技术中使用的毛发生长工具XGen却可以制作出任意形状的头发而且可以精确控制每一根头发和每一个控制点的几何信息。工具Maya XGen 是以任意数量的随机或均匀放置的基本体填充多边形网格曲面的几何体实例化器。XGen 能够以程序方式创建和设计角色的头发、毛发和羽毛。根据Xgen开发的历史生成毛发有种工作模式，一种是基于传统参数化的设置groom模版，一种是交互式修饰工具来控制毛发生长。

具体流程可以参考官方文档

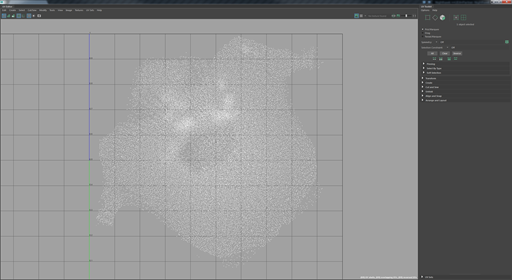
如上图所示，基于Mike的头部模型，分别在不同的区域生长头发，眉毛，睫毛。Xgen最终会记录在哪些几何面片上生长毛发，密度是多少，毛发的长度和弯曲度是多少， 每根头发的粗细是多少。这些头发在Maya里是曲线，Mike的头发在Maya里有超过两万根XGen Spline。考虑到帧率的要求，这些数量的曲线对于实时渲染来说已经是大数据量。

在Maya中制作完成groom后，需要导出几何模型给UE4使用。由于UE4不支持曲线需要在Maya中作如下转换流程：

Xgen Spline ==> Maya Polymesh ==> FBX Polygon

这个转换流程是有UE4对导入模型的要求决定的，UE4支持FBX的导入但是不支持FBX的曲线，所以才会把曲线转成细长的多边形。

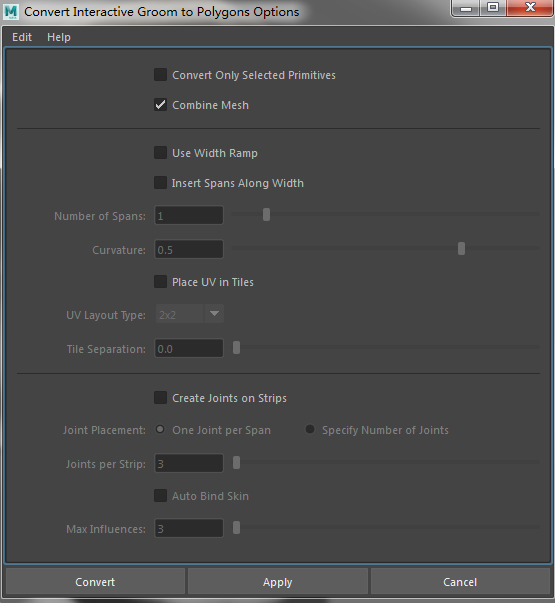
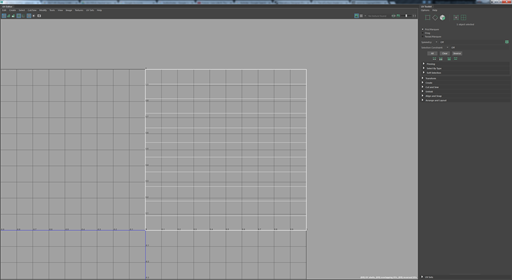
再有了模型后接下来的步骤就是UV几何的设定。头发模型的UV集合设定也是很必要的步骤，根据渲染的需要，头发模型可能需要不同UV集合来控制每根头发的颜色，整体头发的噪音颜色以及头发的烘焙遮挡。Mike的模型根据灯光渲染的需要分成两个UV集合。UV集合1适用于每根头发，所有毛发都从发根到发稍都会按照一定规律来设置UV数值。由于Mike的黄色头发中有白色的头发，这样就需要另外一个可以控制整体的UV集合来控制白色头发的分布。

UV集合1用于设置每根头发的颜色，用于控制从发梢到发尖的颜色过度。每根头发发根的v为0，发稍的v为1.

UV集合2用于控制整体灰色头发中白发的分布，所有毛发没有uv重叠这样更加精准的控制白发。

3. 毛发渲染

3.1 Marschner Hair

经典的毛发渲染模型Marschner Hair。参考文章可以在Cornell大学的网站上找到。

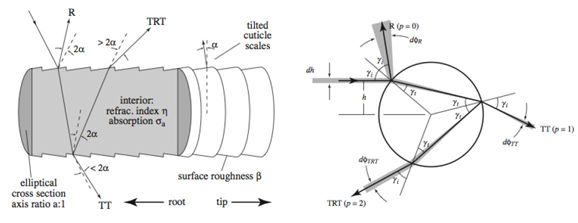
模型示意图如下：

• R ：在头发表面的反射

• TT ：在头发里经过一次光线游走的投射

• TRT ：在头发里经过两次光线游走的折射

• M : longitudinal scattering functions （纵向散射函数）

• N:  azimuthal scattering function (方位角散射函数）

用于计算散射的几何示意图如下：

差角度计算如下：

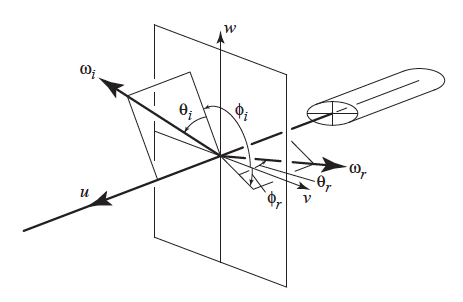
Theta_d = (theta_r - theta_i) /2

Phi = (Phi_r - Phi_i)

半角度计算如下：

Theta_h = (theta_r + theta_i) /2

Phi_h = (Phi_r + Phi_i) /2

R,TT, TRT三种散射纵向散射函数M都满足Theta_h符合高斯分布。公式如下：

Mr = g(Beta_R, Alpha_R, Theta_h)

Mtt = g(Beta_TT, Alpha_TT, Theta_h)

Mtrt = g(Beta_TRT, Alpha_TRT, Theta_h)

R和TRT散射方位角散射函数N分别简化为Cosphi2，TT散射方位角散射函数N满足Phi 符合高斯分布。公式如下：

Nr = Cosphi2

Ntt = g(Gamma_TT, 0.0f, PI - Phi)

Ntrt = Cosphi2

散射公式如下：

S = SR + STT + STRT,

Sp = Mp x Np for P = R, TT, TRT

不同灯光角度的直接光照渲染结果如下：

3.2 非物理真实的多散射

fake scattering （非物理真实的散射）出于性能的考虑，UE4默认给头发加了一个类似于diffuse的非物理真实的散射。渲染结果如下图

3.3 dual scattering

基于物理真实的双向散射模型是毛发多散射的快速估计。和离线光线跟踪毛发间接采样方法相比，双向散射会节省大量时间，质量几乎接近。参考连接

毛发双向多散射模型多用于电影领域离线渲染，腾讯团队将这个模型引入到UE4实时渲染领域。

3.3.1 概念

双向散射主要用于估计毛发的多散射函数，这个函数有两个部分组成：全局散射函数和局部散射函数。全局散射函数用于计算由于光穿过周边的毛发对当前毛发的散射贡献，局部散射用于计算由于光多次在周边头发折射对当前毛发的散射贡献。这两种贡献的总和称为双向多散射。这种计算模型不收光源数量和类型的限制。

3.3.2 UE4中设计和实现

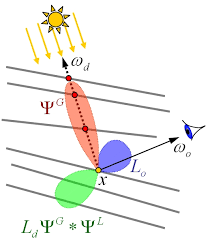
结合光栅化渲染的特点我们采用模型数据预计算的方法将大量数据存存储在贴图中。模型的预计算不会守到颜色和几何数据的限制，也不会收到光源方向的限制。

根据双向多散射的数学理论，我们对以下信息进行预计算

A_bar_f -- 平均前向衰减

A_bar_b -- 平均后向衰减

A_b -- 平均后半球衰减

Alpha_f -- 平均前向散射偏移

Alpha_b -- 平均后向散射偏移

Beta_f -- 平均前向散射方差

Beta_b --  平均后向散射方差

Sigma_b -- 后向散射方差总和

Delta_b -- 平均后向纵向散射函数偏移

N_G_R -- 方向角散射函数R

N_G_TT -- 方向角散射函数TT

N_G_TRT -- 方向角散射函数TRT

B_R -- 散射函数R

B_TT -- 散射函数TT

B_TRT -- 散射函数TRT

K_R -- 吸收函数R

K_TT -- 吸收函数TT

K_TRT -- 吸收函数TRT

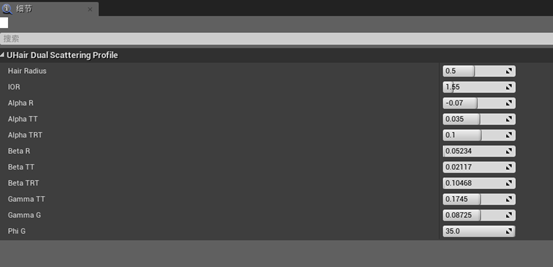
在UE4中把散射模型的预计算设计成参数化控制的Profile, UI如下图所示。这样的优点是用户更容易控制和重复使用。

在UE4动态计算着色的过程中，根据预计算的中间信息按照双向散射计算的理论计算全局散射和局部散射。过程伪码如下：

Dual Scattering的渲染结果如下：

3.3.3 两种散射结果比较

左图是非物理真实的散射，右图是基于物理真实的双向多散射。

参考文献:

[1] LOKOVIC T., VEACH E. : Deep shadow maps. In Proceedings of SIGGRAPH 2000 (2000), ACM        Press/ACM SIGGRAPH, pp. 385–392.

[2] MARSCHNER S. R., JENSEN H. W., CAMMARANO M., WORLEY S., HANRAHAN P. : Light         scattering from human hair fibers. ACM Trans. Graph. 22 (July 2003), 780–791.

[3] MOON J. T., MARSCHNER S. R. : Simulating multiple scattering in hair using a photon mapping   approach. ACM Trans. Graph. 25 (July 2006), 1067–1074.

[4] ZINKE A., RUMP M., LAY T., WEBER A., ANDRIYENKO A., KLEIN R. : A practical approach for          photometric acquisition of hair color. ACM Trans. Graph. 28 (December 2009), 165:1–    165:9.

[5] ZINKE A., YUKSEL C., WEBER A., KEYSER J. :Dual scattering approximation for fast multiple scattering in hair. ACM Trans. Graph. 27 (August 2008), 32:1–32:10.