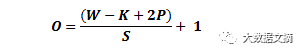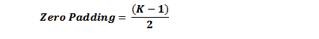步长？填充？池化？教你从读懂词语开始了解计算机视觉识别最火模型

大数据文摘作品，编译 | 马卓群，元元，keiko，钱天培

在上周，我们为大家带来了一篇卷积神经网络的入门介绍：《卷积？神经？网络？教你从读懂词语开始了解计算机视觉识别最火模型 | CNN入门手册（上）》，相信大家已经对卷积神经网络有了初步的了解。这周，我们将更深入地介绍卷积神经网络（以下简称“ConvNets”），解释上周我们提到却又没有细讲的一些概念 。

声明：我在这部分介绍的一些主题非常复杂，完全可以单独列出来写成一篇文章。为了在保证内容全面性的同时，保持文章的简洁明了，我会提供原研究论文的链接供大家参考，这些论文对我讨论的主题有更详细的解释。 

首先，让我们回过头来看看我们的之前介绍的卷积层。还记得过滤器，感受域，卷积吗？如果不记得的话，请回顾本系列的上集《卷积？神经？网络？教你从读懂词语开始了解计算机视觉识别最火模型 | CNN入门手册（上）》。

现在，我们可以通过改变2个主要参数来修改每个层的表现行为。在选择过滤器的尺寸后，还要选择步长和填充。

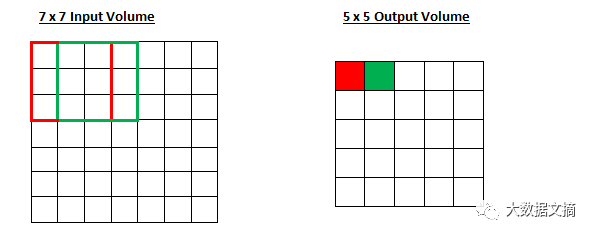
步长控制着过滤器如何对输入量进行卷积。在第一部分的例子中，过滤器是通过一次移动一个单位来对输入量进行卷积的，而这个器移动单位就是步长。（在这种情况下，步长即为1。）我们通常选择的步长会确保输出量是整数，而非分数。让我们看一个例子，想象我们有一个7×7的输入量，一个3×3的过滤器（为了更加简明，这里我们忽略第三维度），步长为1。这是情况相信大家已经很熟悉了。

老一套，对吧？看看你是否能猜出，随着步长增加到2，输出量将会发生什么变化。

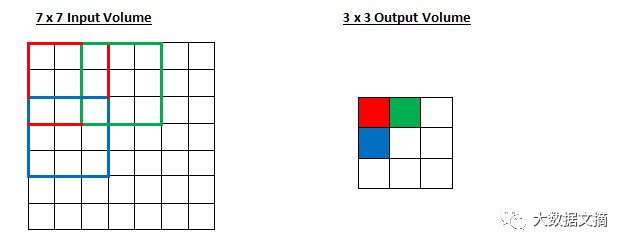
图为步长为2时卷积的输出情况

所以，正如你所看到的，感受域现在一次移动了2个单位，输出量也缩小了。请注意，如果我们试图将步长设为3，当我们进行到最后一行/列，我们就会遇到感受域无法与输入量完全重叠、有空白余留的问题。通常，如果希望在感受域有更少地重叠、保持较小的空间维度，程序员们就会增加步长。

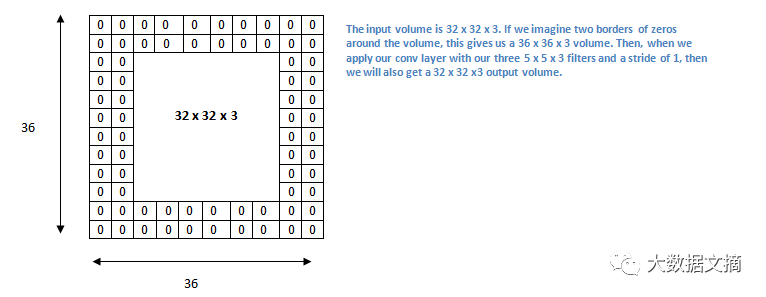
现在，让我们看看填充。在开始之前，让我们先想一个场景。当你把三个5×5×3个过滤器应用到一个32×32×3输入量时会发生什么？输出量将会是28×28×3。请注意，空间维度会减少。当我们继续应用卷积层的时候，量的大小将减少得比我们想像的更快。在学习网络的早期层中，我们希望最大化地保存原始输入卷的信息，以便我们提取那些低层次的特征。比如说我们要运用同样的卷积层，但同时我们想要让输出量保持在32 x 32 x 3。要做到这一点，我们可以对该层加一个大小为2的零填充。零填充就是对输入量在边界上用零进行填充。如果我们考虑2个零填充，那么我们就有了一个36×36×3的输入量。

如果你的步长为1，并且把零填充的大小设置为

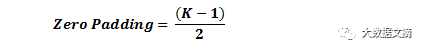
其中，K是过滤器大小，那么输入量和输出量将始终保持相同的空间维度。

对于任何一个定卷积层，输出尺寸的计算公式如下：

其中，O是输出量的高度/长度，W是输入量的高度/长度，K是过滤器的大小，P是填充大小，S是步长。

那么，我们要怎么知道应该用多少神经网络层、其中有多少卷积层、过滤器的尺寸是什么，以及步长和填充的值是多少呢？这些都不是无关紧要的问题，但也没有一套公认的标准。这是因为网络的选取将在很大程度上依赖于您所拥有的数据类型。数据会因为图像的大小、复杂度、图像处理任务的类型不同而变化。当你分析数据的时候，一个选择超参数的方式就是，寻找能创造出图像抽象的合适尺寸组合。

根据传统惯例，在每个卷积层后，我们会紧跟着应用一个非线性层（或激化层）。没有这个非线性转化，整个系统基本上就是在卷积层中进行线性操作（只是元素频繁的的乘法和加法）。在过去，我们通常使用的是非线性函数，比如tanh 函数和sigmoid函数，但研究人员发现ReLU层在不牺牲精确度的前提下加快网络的训练速度，从而带来更好的运作效果。同时，它也有助于缓解梯度消失问题。这个问题指的是，在经过每一层后，梯度会指数性地递减，因而低层的网络训练会变得非常慢。（对这个问题的详细解释已超出了这篇文章范围，如果想看进一步的解释，请参照链接1、链接2

ReLU层将函数f（x）= max（0，x）应用于所有的输入值。基本上，这一层就是把所有的负激活变为0。这一层提高了模型中的非线性特性和整个网络，并且不影响感受野的卷积层。

这篇由伟大的Geoffrey Hinton而著（又名深度学习之父）的文章更详细的阐释了ReLu的优点。

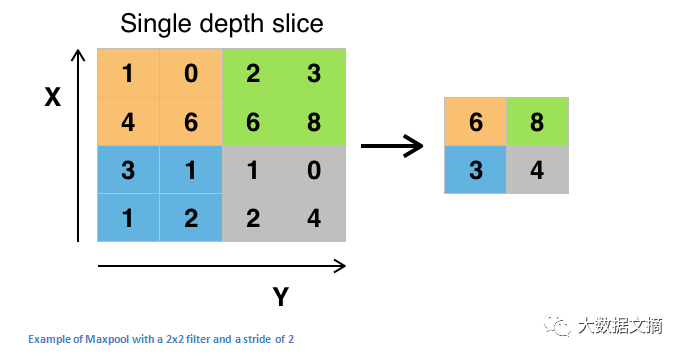
在应用了一些ReLU层之后，程序员可以选择应用池化层。它也被称为向下采样层（downsampling layer）。在不同池化层中，最大值池化(maxpooling)是最受欢迎的。先用一个过滤器（通常大小2x2）和一个相同长度的步长。将其应用于输入量，然后在每一个分区输出最大数字 。

另外几种池化层的类型包括平均池和L2规范池。池化层背后的直观原理是，一旦我们知道原始输入量中（这里将会有一个高激活值）有一个特定的特征，那么它的确切位置，就没有它相对于其他特征的位置那么重要了。所以，你可以想象，这一层是如何极大地减少了网络的空间维度的（长度和宽度的变化，深度不变）。这可以帮助实现两个目的。首先，参数（或者权重）的数量减少了75%，从而降低了计算成本。其次，我们也可以借此控制过度拟合。 

过度拟合这个术语指的是，一个模型过于贴近训练示例，而导致不能很好地拟合验证集和测试集。过度拟合的一个典型症状就是，训练好的一个模型在训练集上可以达到100% 或 99% 拟合，而在测试集上却只能达到50%

现在来看看丢弃层。丢弃层对于神经网络而言有特殊作用 。在上一个部分，我们讨论了过度拟合的问题，即训练之后神经网络的权重参数过于贴近训练示例，以至于在新示例上的表现欠佳。丢弃层的想法本质上是很简单的。在这一层随机把几个激发点设置为零，从而“丢弃”他们，如此而已。这样一个看起来不必要而反常的简单过程有什么好处呢？一方面，这个过程促使神经网络变得“冗余”。这里冗余的意思是指，即使神经网络失去了一些激发点，还是能够提供正确的分类结论或者输出特定的示例。另一方面也确保神经网络没有过度拟合训练集，从而减轻过度拟合的问题。这里重点强调一下，丢弃层只是在训练过程中出现，而并不在测试过程中出现。

更多信息请参见Geoffrey Hinton 所著相关文献。

网中网层是指一个采用1x1过滤器的卷积层。乍一看你可能会有疑问，感受域的范围通常要大过输出值的特征图，那么网中网究竟有什么作用呢？回想一下，这些1x1的卷积是有一定深度的，我们可以把它设想为1x1xN的卷积，其中N是在这层上过滤器的个数。实际上，网中网层是做了一个N维元素的对应相乘，其中N是层中输入的深度。 

Min Lin 所著相关文献对网中网层进行了更详细地阐述。

在CNN入门手册（上）（加入链接）中，我们讨论过给图片物体分类这一任务。在这个过程中，我们先输入一张图片，然后从一串类别中输出图片物体对应类别的序号。但是，对于物体定位这样的任务而言，我们的目的不仅是得到分类序号，还要在图片中用边框指出物体的位置。

除此之外，我们还可能碰到物体检测的任务，这需要对图片上的所有物体进行物体定位。因此，我们会得到多个边框以及多个分类标签。 

最后，我们还有细分物体的任务，其目的是输出分类标签和图片中所有物体的细节轮廓。

在CNN入门手册（下）中，我们会讲更多完整这些任务的细节，如果你已经急不可耐了，可以参阅下面的参考资料。

检测/定位、细分

是的，还有更多的参考材料没有被列举出来。

目前，深度学习圈子里有一个常见的误区，即如果没有谷歌式的海量数据，你就不可能做出一个有效的深度学习模型。虽然数据是创建神经网络的重要部分，但是迁移学习的思路可以减少数据的需求量。迁移学习的做法是采用一个预训练好的模型（别人用大量数据训练得到的神经网络的权重和参数），再用自己的数据微调模型。这个思路利用了预训练的模型进行特征提取。你需要把原来神经网络的最后一层去掉，换成你自己的分类标签（取决于你的问题空间），接着保持其他层的权重不变，正常地训练神经网络模型（保持其他层不变意思是在梯度下降/最优化的过程中不改变其他层的权重）

我们来讨论一下为什么这个方法可行。比如说我们用ImageNet（ ImageNet是一个包括了超过1000类1400万张图片的数据集）训练得到预训练的模型。考虑一下神经网络模型的低层，我们知道低层部分会检测到诸如边缘和曲线这样的特征。现在，除非你的问题空间和数据集很独特，你的神经网络模型也会需要检测曲线和边缘特征。与其从随机权重初始值开始训练整个神经网络，我们可以采用预训练模型的权重（并保持这部分权重不变），然后重点对重要层（更高的层）进行训练。如果你的训练集数据与ImageNet差异很大，你可以只固定低层部分中的几层，用自己的数据训练更多层。

• Yoshua Bengio 所著的参考文献（另一个深度学习的大师）

• Ali Sharif Razavian 所著的参考文献

• Jeff Donahue 所著的参考文献

数据增强技术

到目前为止，我们对卷积神经网络中数据的重要性大概还是模糊不清的。事实上，海量的数据对卷积神经网络的训练是十分重要的。（当然了，迁移学习可以在一定程度上弱化我们对数据量的要求。）那么最后，就让我们来讨论如何通过几个简单的变换增加已有的数据量吧。正如我们之前提到过的，当一个计算机处理一个图片输入时，它会读入一个像素值数组。如果整个图片都向左移动了一个单位，对于你我来说，这个变化是感觉不到的。然后，对于一个计算机而言，在分类和图片标签不变而像素数组改变的情况下，这个移动可能会造成很大的影响。在改变训练数据表示的同时固定分类标签的这种方法，被称为数据增强技术，这是一种人为扩展数据集的方法。一些常用的数据增强方法有调成灰度(grayscales)，水平翻转(horizontal flips)，竖直翻转(vertical flips,)，随机裁剪(random crops), 颜色抖动(color jitters)，平移(translations), 旋转(rotation)等等。如果对训练集的数据进行以上这几种变换，你可以很容易地得到原数据两至三倍的数据量来训练模型。