基于 Nebula Graph 构建图学习能力
经常看技术文章的小伙伴可能会留意到除了正在阅读的那篇文章,在文章页面的正文下方或者右侧区域会有若干同主题、同作者的文章等你阅读;经常逛淘宝、京东的小伙伴可能发现了,一旦你购买或者查看过某个商品之后,猜你喜欢的推荐商品会贴近你刚拔草的商品…这些日常生活中常遇到的事情,可能是由一个名叫图学习的“家伙”提供技术支持。
图学习,顾名思义是基于图的机器学习,按照本期项目介绍的参赛队伍——图学习兴趣小队队长杨鑫的话就是,图学习是一个通过深度学习方法,基于图的结构与属性生成一个向量作为点、边或者整个图的表征。
在之前 Nebula Hackathon 2021 年的参赛项目中,图学习兴趣小队“豪气”地说要让 Nebula Graph 具备支持图学习的能力,在本文接下来的内容中,你将了解到他们是怎么实现这一目标的。
在讲述项目实现之前,项目负责人杨鑫先给大家上了一课“图解图学习”。
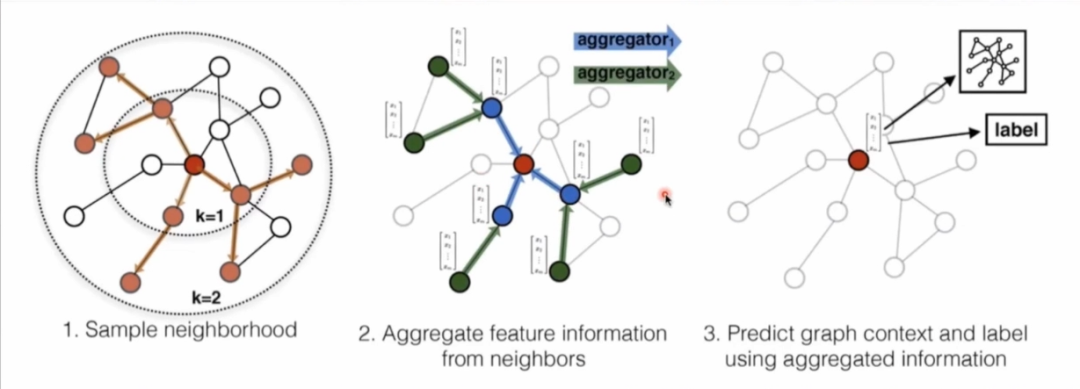
以获取顶点的向量表征为例来讲解下图学习过程,第一步需要对图中顶点邻居进行采样拿到邻居的拓扑结构以及属性;第二步便是通过自定义的聚合函数聚合邻居顶点蕴含的信息进行计算;最后一步基于聚合信息得到图中各顶点的向量表示。
杨鑫表示,衡量一个图学习算法的好坏是通过生成向量中包含图中顶点属性及拓扑结构的丰富程度来判断的。
在选择图学习框架时,图学习兴趣小队有自己的一套选型标准:首先它是开源组件,方便二次开发,其次它支持分布式,最后框架本身和图数据库的耦合程度要低方便定制化开发。经过深入调研,由于 DGL 同底层的图数据库耦合过高,PYG 不支持分布式,最终他们采用了 Euler,而在 Nebula Hackathon 2021 中,图学习兴趣小队的重点工作便是用 Nebula Graph 替换 Euler 原生图数据库,让社区用户可以基于 Nebula Graph 低成本尝试图学习能力。

在方案设计上,架构分为三层:底层是 Nebula Graph 图数据库,中间层是图采样算子层,为上层 Euler 图算法提供多种采样图数据的能力。图采样算子则是他们本次工作的重点——重写 22 个 TF 采样算子、6 种 nGQL 采样语法。
以全局带权采样语法设计为例,
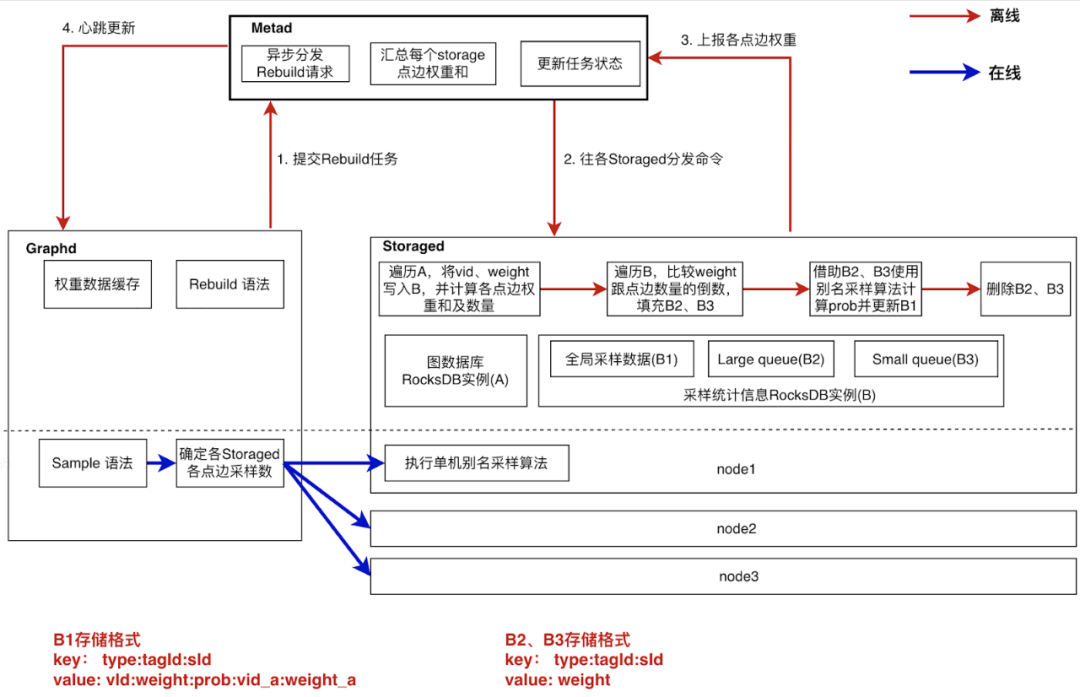
这里采用了预计算(离线)+ 计算下推(实时)的方式来实现全局采样,主要过程为(上图 1-4)
- graphd 提交异步构建任务给 metad;
- metad 下发任务给各个 storaged 节点进行计算;
- storaged 将计算结果上报给 metad 汇总;
- metad 通过心跳将结果同步给 graphd。
详细展开来讲,在图学习训练过程中,数据采样是一个非常高频的操作,采样性能好坏对图学习训练耗时影响很大。
在这里,杨鑫他们采用别名采样算法作为全局带权采样语法的核心算法,它的基本原理是首先对进行采样的全部数据根据各自的权重计算出一份采样表,采样表由行号(sid)、vid1、采样概率(prob)、vid2 四部分组成,其中行号是从 0 开始的编号,vid1、vid2 表示可以被采样的某个顶点的 vid;采样流程是首先在表中随机选择一行,然后再随机生成一个 0~1 之间的值 p,如果 p < prob,则本次采样的数据是 vid1,否则采样 vid2。
目前图学习是基于静态图数据训练,因此我们可以通过预计算的方式离线生成一份别名采样表,而实时采样过程简化为基于预计算的采样表做两次随机采样,时间复杂度由 O(n) 降到 O(1),可以极大地提高采样效率。
下面是基于 Nebula Graph 实现的全局带权采样具体实现,跟 Nebula Graph 的索引重建逻辑很相似。
- Graph 服务调用 Meta 服务启动一个异步构建采样表任务,并支持异步任务的状态查询。
- Meta 服务的作用是控制异步任务的执行,包括分配每个 Storage 节点需要处理的数据(根据 partition 的 leader 分布决定)、异步触发各个 Storage 节点进行采样表的计算、记录任务的执行状态、记录全局信息(点、边权重和)、通过心跳逻辑将全局信息缓存在 Graph 服务中。
- Storage 服务的任务是生成所负责数据的采样表。采样表的计算是整个流程中的核心逻辑,计算过程需要对所有点、边编号,并根据权重大小对点、边进行分类,很显然这些数据是无法全部存储在内存中的,所以我们在 Storage 中增加了一个采样统计信息 RocksDB 实例来存储采样表、点边总数、点边权重、计算中间变量等数据。以计算某一类点的采样表的过程为例:
第一步遍历全图来统计这一类点的权重和数量,同时为了给生成采样表做准备,将点的序号(点的读取顺序)、vid、权重等数据存储在了图中(B1)结构中。其中 key 的数据结构是 type + tagid + sid,type 标识了数据是 B1 类型,tagid 就是点的 tag,sid 是点的序号,跟采样表的 key 结构相同。
第二步将数据分类,根据权重值以点的总数的倒数为界将所有的点分成两部分,分别以(B2)、(B3)的结构存储,key 的组成与 (B1) 结构相比就是type 值不同。
第三步分别遍历(B2)、(B3),根据别名采样算法的理论来计算每个点的采样概率 prob。这里每个点是用 sid 来标识的,也就是说实际上是在计算第 sid 个点的采样概率,概率值作为采样表的一部分会更新到(B1)结构中。
第四步将中间变量(B2)、(B3)结构删除掉,释放磁盘空间。
利用采样表进行实时采样的过程就比较简单了。完成采样表的预计算后会将点、边权重的统计信息上报到 Meta 服务存储,然后通过心跳通知 Graph 服务将这些数据缓存在本地。根据这些数据可以计算出点、边在各 Storage 服务上所占的权重比例,将用户指定的采样数量按比例分配到各 Storage 服务,然后在 Storage 服务上通过两次的随机数操作采样到足够数量的数据后返回,最后在 Graph 服务上进行数据聚合,这样就完成了一次带权采样。
另外为了提高异步任务的健壮性,还实现了失败重试、任务重复限制、重建采样表后脏数据清理、导出采样表等功能。
提到项目设计以及重写其他算子过程中遇到的问题,图学习兴趣小队队长杨鑫表示因为 Nebula Graph 的数据都存储在磁盘中,要用 Nebula Graph 替换 Euler 原生内存图数据库,改造后的 Euler 在采样效率上肯定要低于原生 Euler,因此怎么保证改造后 Euler 的图学习训练耗时尽可能接近原生 Euler 是要解决的首要问题,至少得保证两者采样性能不能有数据级上的差距。
原生 Euler 中的图学习算法由 Python 实现,通过 TensorFlow 的 OP 机制来调用 C++ 实现的采样算子,然后在采样算子内直接调用内存图数据库获取数据,这样就完成了一次数据采样。
图兴趣小队最初的方案是将采样算子用 Python 实现,这样一次数据采样过程就变成了图学习算法直接调用采样算子,然后在采样算子内则通过 Nebula Graph 的 Python 客户端执行采样语法获取数据。这样改造后的系统会有更清晰的处理流程,但是经过测试他们发现其训练耗时要远大于原生 Euler,具体到训练过程中的每次数据采样上,其耗时是原生 Euler 的几十倍,这样的结果显然是不能满足要求的。通过分析各阶段执行耗时他们发现,数据采样的耗时要远大于采样语法的执行耗时,所以他们认为是 Python 客户端在反序列化上消耗了大量时间。因此图兴趣小队进行了第一次优化,使用 fbthrift fastproto 替换 Nebula Graph 原生客户端的序列化组件,优化后的性能提高了一倍,整体训练耗时确实有所降低,但是这样的结果却仍然无法满足他们的使用要求。
这时候用上了第二个方案,重写 C++ 版本的采样算子,在采样算子中通过 Nebula Graph 的 C++ 客户端执行采样语法获取数据,相比第一个方案多了一些适配工作,算子的重写主要是适配 C++ 客户端的输入输出,另外改造了 C++ 客户端以便采样算子的调用。
这也是他们最终的方案,这样改造后的 Euler 虽然在训练耗时上仍然高于原生 Euler,但是差距控制在了二倍以内,符合预期。
当谈到本次有什么值得图学习兴趣小队留意的项目时,队长杨鑫表示比较关注的是大油条东北虎队伍的项目——如何吊打 Nebula 的深度查询,这个项目的优化思路对他们很有借鉴意义。
因为在实际使用中,图兴趣小队所在团队的业务方有很多的多跳查询需求,包括 GO 查询、FINDPATH 查询等。这本应该是 Nebula Graph 所擅长的部分,在大部分场景下也确实如此,但是在遇到出度很大的顶点的时候,查询性能会急剧恶化。其主要原因还是基于目前 Nebula Graph 的架构,多跳查询只能先将一跳的结果集汇总到 Graph 服务后才能进行下一跳计算,完全不能将多跳计算下推。而这个项目正好给他们提供了一个解决这个难题的思路。






















