【数据挖掘算法分享】机器学习平台——回归算法之线性回

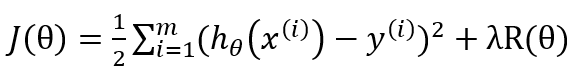
其中J（θ）， 为W^T*X和Y的函数。目标函数包含两部分内容，正则项用于控制模型的复杂度（最小化结构风险函数），损失用于度量拟合误差（通常使用均方误差），目标函数通常为w的凸函数。正则项参数 λ>0（regParam）为最小化误差和模型复杂度之间提供了一种折中（如，用来避免过拟合）。

线性回归算法的整个步骤如下：

（1）给定训练数据样本集

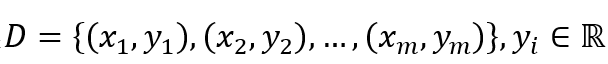
选取初值θ0，给定收敛容差 ε，最大迭代次数K，然后解下面优化问题：

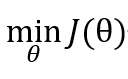
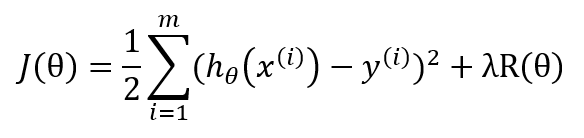
（2）采取下面公式更新θ

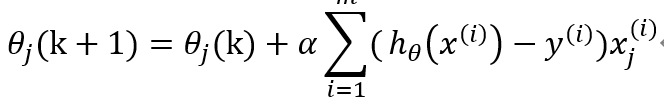
（3）当或者k<K ,输出θ，否则转步骤2.

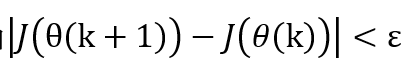
（4）构造回归决策函数

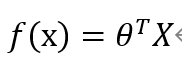
线性回归适合分布式实现，能支持大数据量建模。

线性回归算法假设每个影响因素与目标之间是线性关系，并通过特征选择，得到关键影响因素的线性回归系统。该算法是利用数理统计中回归分析，来确定两种或两种以上变量间相互依赖的定量关系的一种统计方法，通过凸优化的方法进行求解。在实际业务中应用十分广泛。下面演示下Tempo机器学习平台中线性回归算法的使用方法。

数据格式

必须设置类属性（输出），且类属性（输出）必须是连续型（数值）；

非类属性（输入）可以是连续型（数值）也可以是离散型（名词）；

参数说明

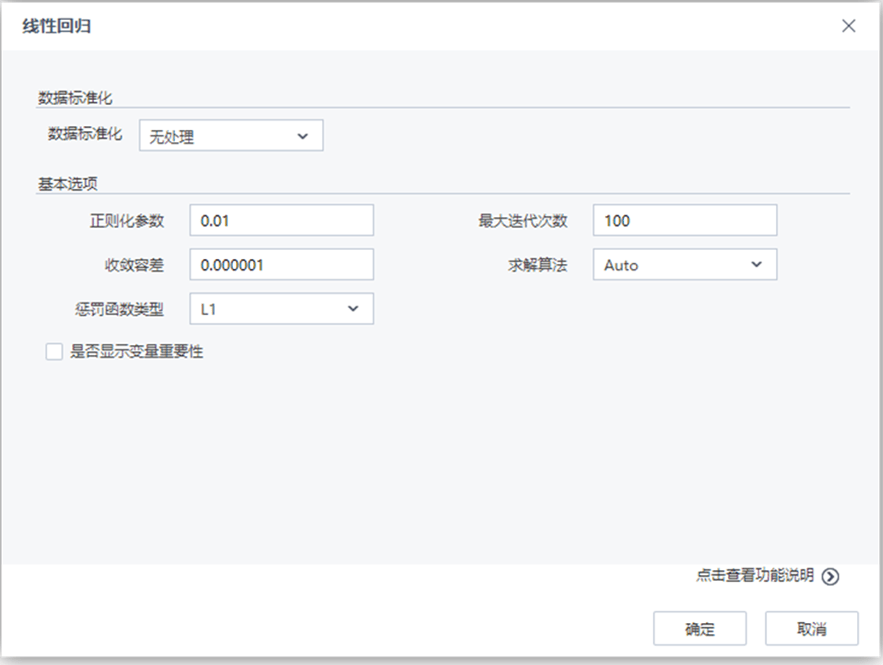
参数 类型 描述 数据标准化 下拉框 设置数据标准化的方法，字符型，取值范围：无处理，归一化，标准化，默认值为无处理 取值区间下限 文本框 设置归一化取值区间下限，浮点型，取值范围：[0,∞)，默认值为0 取值区间上限 文本框 设置归一化取值区间上限，浮点型，取值范围：[0,∞)，默认值为1 正则化参数 文本框 正则化参数控制机器的复杂度，浮点型，取值范围：[0,∞)，默认值为0.01 收敛容差 文本框 设置终止迭代的误差界，浮点型，取值范围：[0,∞)，默认值为0.000001 最大迭代次数 文本框 设置最大迭代次数，整型，取值范围：[1,∞)，默认值为100 罚函数类型 下拉框 设置惩罚函数类型，0对应L2罚函数，1对应L1罚函数，(0,1)之间对应L1和L2的组合罚函数。浮点型，取值范围：[0,1]，默认值为0 求解方法 下拉框 选择线性回归的求解方法，文本型，取值范围：Auto，L-BFGS,Normal （Normal->加权最小二乘法，L-BFGS->牛顿法，Auto->算法自动选取（L-BFGS,Normal）中的一种）。默认值为Auto 是否显示变量重要性 复选框 用户选择是否分析每个变量对于回归结果的影响程度，如果选择是，则在洞察中显示参与建模的每个变量对于模型的贡献程度情况

结果说明

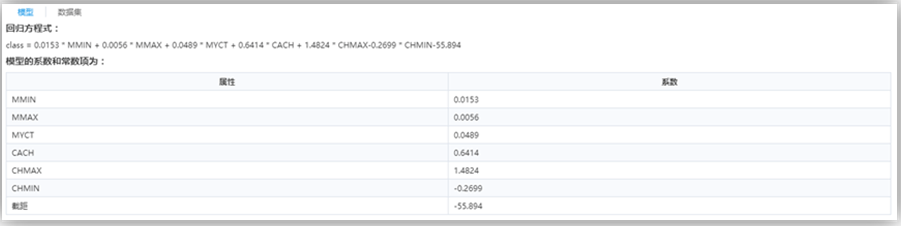
线性回归的方程及其系数。

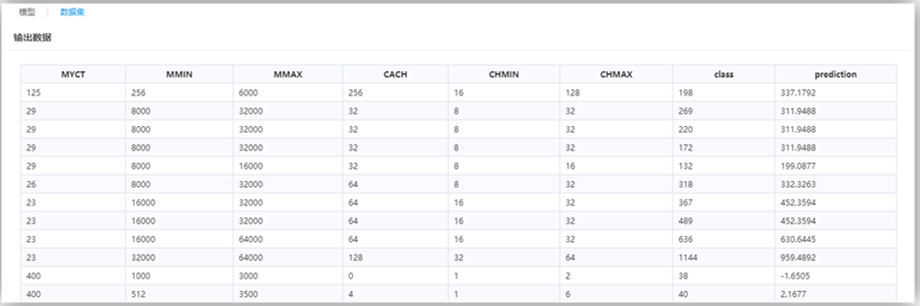
最后一列属性“prediction”为回归预测列。

演示示例

构建如下流程：

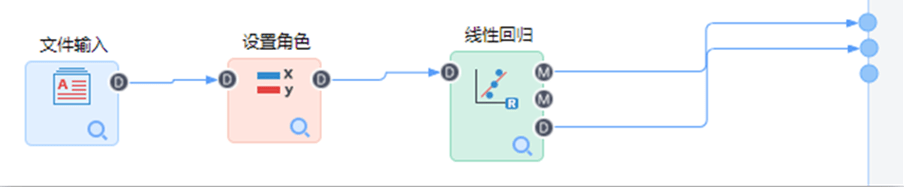
【文件输入】节点配置如下：

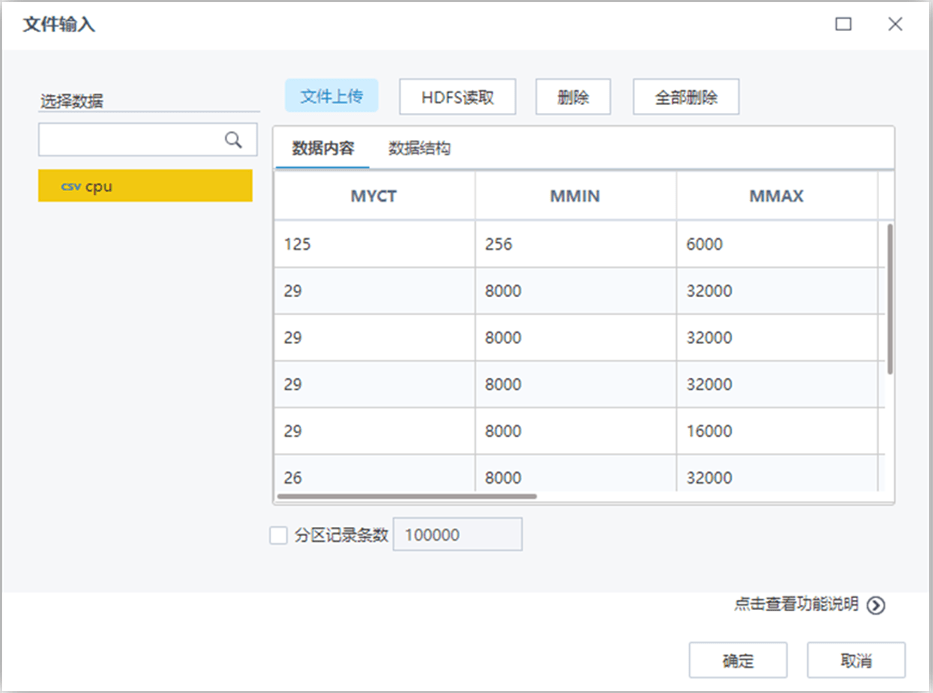
【设置角色】节点配置如下：

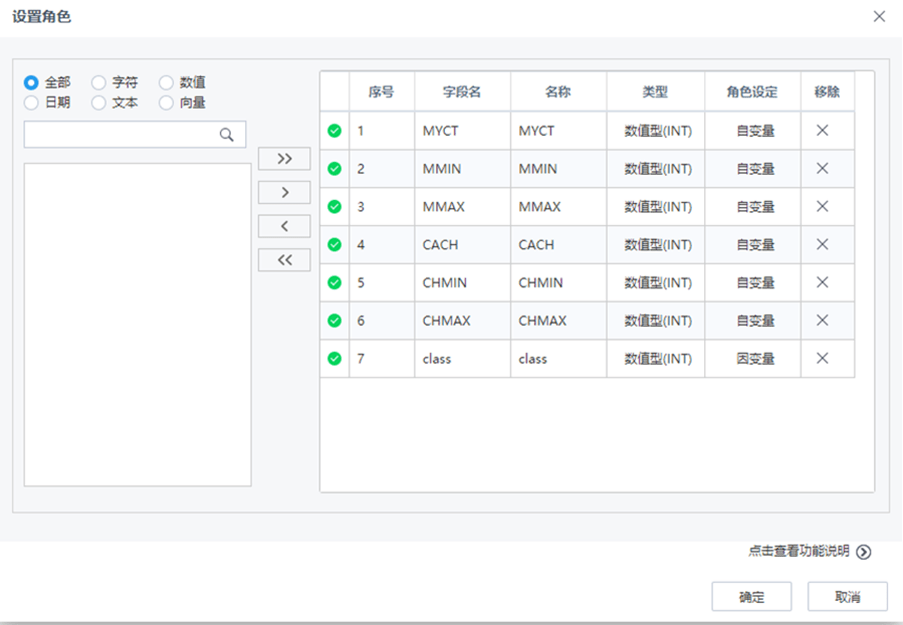
【线性回归】节点配置如下：

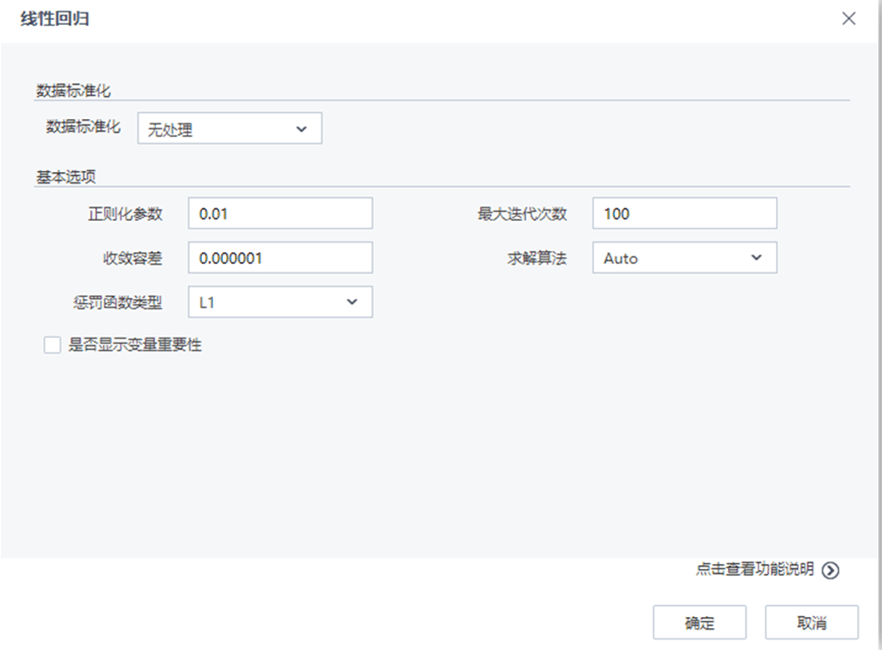
流程运行结果如下：