质量工具之故障树分析FTA

FTA的数学基础

我们前文提到，故障树分析FTA可以用于系统设计、安全分析甚至是根本原因分析，既可以做定性分析又可以做定量分析，是全能型的分析技术。

故障树分析的基础工具是故障树图，从特定的故障事件开始， 利用故障树考察可能引起该事件发生的各种原因事件及其相互关系。

故障树通过事件符号和逻辑门符号表达事件、原因及其相互关系，是一种利用布尔代数(又称布尔逻辑) 符号演绎地表示特定故障事件 发生原因及其逻辑关系的逻辑树图。

为了进行故障树的定性分析和定量分析，需要建立故障树的数学模型，写出它的数学表达式。

布尔代数是故障树分析的数学基础。布尔代数是集合论的一部分，是一种逻辑运算方法 它特别适合于描述仅能取两种对立状态之一的事物。

故障树中的事件只能取故障发生或不发生两种状态之一，不存在任何中间状态，并且故障树的事件之间的关系是逻辑关系，所以可以用布尔代数来表现故障树。

 

 

集合的基本概念

· 集合：简称集，是现代数学中一个重要的基本概念。集合是“确定的一堆东西”，是指具有某种特定性质的具体的或抽象的对象汇总而成的集体；集合里的“东西”是构成集合的对象，这些对象则称为集合元素。

现代的集合一般被定义为：由一个或多个确定的元素所构成的整体。从最普遍的意义上说，具体确定的可以区分的若干事务(事项、事件)的全体就是集合，其中的事务叫做元素。

通常用大写字母如A、B、S、T、...表示集合，而用小写字母如a、b、x、y、...表示集合的元素。

比如，鱼骨图中，六个主刺元素 {Man, Machine, Material, Method, Measurement, Enviroment} 构成原因Causes的集合，每个主刺下可以再分很多小刺形成子集。

o 空集不包含任何元素，记为∅。空集是特殊的集合。

o x是缺陷集合A的元素，则称x属于A，记作x∈A。

o y不是缺陷集合A的元素，则称y不属于A，记为y∉A。

o 集合A中元素的个数为集合中的元数，记作|A|。

o 集合中的元素不能重复出现，集合中的元素无顺序之分。

· 集合的表示方法：

集合有如下几种表示方法：

o 列举法，列出集合的所有元素，并用花括号括起来。

例如，在质量管理软件QMS中，某公司质量部分别收集某个系列的两个产品在一个月内发生的缺陷类型，其缺陷集合分别是A和B，A={a，b，c，d，e，x}，B={f，b，g，d，h，y}。

 

 

o 描述法，将集合中元素的共同属性描述出来。

例如，在质量管理软件QMS中，设所有特殊特性的集合为T，关键特性、重要特性和一般特性的集合分别是C、S和G，则C={x|x∈T}。

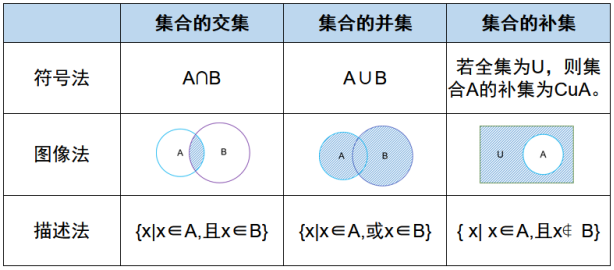
o 图像法，是一种利用二维平面上的点集表示集合的方法。一般用平面上的矩形或圆形表示一个集合，是集合的一种直观的图形表示法。

o 区间法，用数轴、无穷大、无穷小、开区间、闭区间 、半开半闭区间表示。数学分析中，最常遇到的实数集的子集是区间。

o 符号法，有些集合可以用一些特殊符号表示。例如，R：实数集合(包括有理数和无理数)；∅：空集(不含有任何元素的集合)。

 

 

· 有限集和无限集：集合中元素的数目称为集合的基数，集合A的基数记作card(A)。当其为有限大时，集合A称为有限集，反之则为无限集。 一般的，把含有有限个元素的集合叫做有限集，含无限个元素的集合叫做无限集。

· 交集：由属于A且属于B的相同元素组成的集合，记作A∩B(或B∩A)，读作“A交B”(或“B交A”)，即A∩B={x|x∈A，且x∈B}。注意交集越交越少。若A包含B，则A∩B=B，A∪B=A。

例如，上面A和B两个缺陷集合的交集A∩B={b，d}。

· 并集：由所有属于集合A或属于集合B的元素所组成的集合，记作A∪B(或B∪A)，读作“A并B”(或“B并A”)，即A∪B={x|x∈A,或x∈B}。注意并集越并越多，这与交集的情况正相反。

例如，上面A和B两个缺陷集合的并集A∪B={a，b，c，d，e，f，g，h，x，y}。

 

 

 

· 子集：设S，T是两个集合，如果S的所有元素都属于T，即x∈S ⇒ x∈T，则称S是T的子集，记为S⊆T，读作“S含于T”。 符号⊆读作“包含于”，表示该符号左边的集合中的元素全部是该符号右边集合的元素。对任何集合，都有S⊆S，∅⊆S。

o 相等集合：如果集合X是集合Y的子集，且集合Y是集合X的子集，此时，集合X与集合Y中的元素相同，因此集合X与集合Y相等。

o 空集∅是任何一个集合的子集。

· 真子集：如果M是N的一个子集，即M⊆N，但在N中存在一个元素p不属于M ，即M⊊N，则称M是N的一个真子集。

o 空集∅是任意一个非空集合Ω的真子集。

· 补集：一般指绝对补集。

假设质量管理软件中的某个系列产品的所有缺陷的集合为F，那么A和B都是F的一个子集，由F中所有不属于A或B的元素组成的集合，叫做子集A或B在F中的绝对补集。

在集合论和数学的其他分支中，存在补集的两种定义：相对补集和绝对补集。

1）相对补集：针对缺陷集合A和B，由属于A而不属于B的元素组成的集合，称为B关于A的相对补集，记作A-B或A\B，即A-B={ x| x∈A,且x∉B}={a，c，e，x}。

2）绝对补集：假设某公司产品缺陷的全集为U，有A⊆U，则A关于全集合U的相对补集称为A的绝对补集(或简称补集)，记作A'或~A或CuA。

· 幂集：针对缺陷集合A，由集合A所有子集组成的集合，称为集合A的幂集，记作2A={ x| x⊆A} [注：也有记作P(A)或CuA]。对于幂集有定理如下：若集合A是由n个元素所组成的有限集合，A的幂集的基数等于2的有限集A的基数次幂。

 

 

布尔代数运算法则

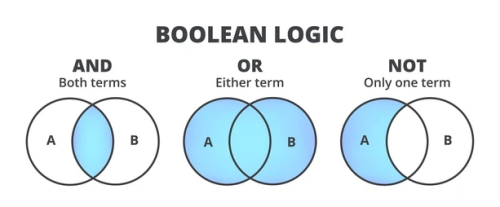
在布尔代数中， 与集合的“并” 相对应的是逻辑和运算，记作”+“；与集合的“交” 相对应的是逻辑积运算，记作”·“。

故障树中的逻辑或门(OR)对应于布尔代数的逻辑和运算，两个事件为并联； 逻辑与门(AND)对应于逻辑积运算，两个事件为串联。

传统的加减乘除四则运算反映的是事物间的数量关系，而布尔运算则反映的是事物间的因果关系。与普通代数四则运算一样，布尔代数的运算也遵循基本的运算法则。

布尔代数中的变量代表一种状态或概念，数值1或0并不是表示变量在数值上的差别，而是代表状态与概念存在与否的符号。布尔代数主要运算法则有：结合律，交换律，分配律，吸收律，幂等律等。

下面列出了故障树分析中常用到的布尔代数运算法则：

交换律：A·B=B·A；A+B=B+A；

结合律：A·(B·C)=(A·B)·C；A+(B+C)=(A+B)+C；

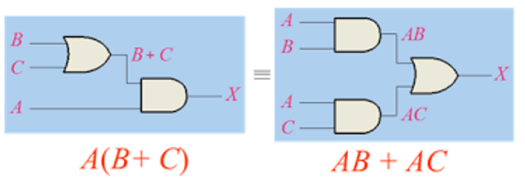
分配律：A·(B+C)=A·B+A·C；A+(B·C)=(A+B)·(A+C)；

吸收律：A·(A+B)=A；A+A·B=A；

 

 

幂等律：A·A=A；A+A=A；

互补律：A·A'=∅=0；A+A'=Ω=1；

对合律：(A')'=A；

重叠律：A+A'B=B'+BA=A+B；

摩根定律：(A+B)'=A'+B'；(A·B)'=A'+B'

 

布尔代数表达式的简化

把故障树中连接各事件的逻辑门用相应的布尔代数逻辑运算表现， 就得到了故障树的布尔表达式。 一般地， 可以自上而下地把故障树逐步展开， 得到其布尔表达式。

从上面布尔代数运算法则的介绍中，我们不难发现，等式两边的表达式虽然不同，但却是等价的，逻辑功能是相同的。

也就是说，同一故障树可以有不同的表达形式，每一表达式都可以画出与其相应的逻辑图。

逻辑表达式最简单的标准有两个：一是所含乘积项的个数最少；二是在前一条件下，每个乘积项中变量的个数也最少。

常用的化简方法有两种：代数法和卡诺图法。

1. 代数法

代数法，又叫公式法，利用布尔代数的基本运算法则，对较复杂的布尔代数式进行演算化简的方法。如何使布尔代数式达到最简，在很大程度上依赖人们对布尔运算掌握的熟练程度和实践经验。下面是几种常用的化简方法。

1）并项法

利用互补律：A+A'=1，并项后消去变量。

例如：Y = A·B·C+A'·B·C = (A+A')B·C = B·C

2）吸收法

利用吸收律：A+A·B=A，吸收多余项，消去多余变量。

例如：Y = A·B+A·B·C = (A·B)+(A·B)C = AB，或 Y = A·B(1+C) = A·B；

 

 

3）消去法

利用吸收律、分配律、摩根定律等消去多余因子。

例如：Y = A·B+A'·C+B'·C = A·B+(A'+B')·C = A·B+(A·B)'·C = (A·B)+(A·B)'·C = A·B+C

4）配项法

利用互补律A+A'=1，A+1=1等，先把一项拆成两项，再重新与其他项组合进行化简，消去更多的项。

例如：Y = A·B+B·C+(A·C)' = A·B(C+C')+B·C+A·C' = A·B·C+A·B·C'+B·C+A·C' = (A+1)B·C十A·C'(B+1) = B·C+A·C'

通过代数法化简表达式，没有一个固定的模式，往往要综合运用多种方法，逐步积累经验才能运用自如。

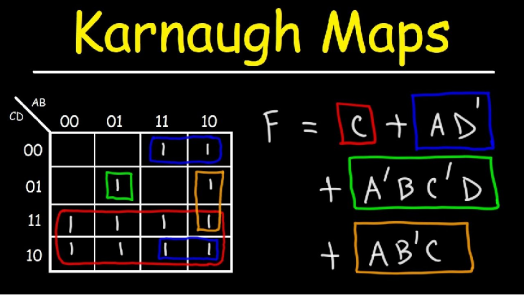
2. 卡诺图法

用代数法化简布尔表达式，需要依赖经验和技巧，有些复杂表达式，很难通过代数法求得最简形式。

卡诺图化简法是一种更加系统并有统一规则可循的逻辑函数化简法，它是逻辑函数的最小项按相邻关系排列的方格图，具有几何直观性这一明显的特点，在变量较少(不超过六个)的情况下比较方便，且能得到最简结果。

此法由卡诺(M.Karnaugh)于1953年提出，感兴趣的读者可以自行查阅资料了解。